
向
伟大的数学家 欧拉
致敬!
莱昂哈德·欧拉(Leonhard Euler ,1707年4月15日~1783年9月18日),
瑞士数学家、自然科学家。
1707年4月15日出生于瑞士的巴塞尔,1783年9月18日于俄国圣彼得堡去世。
欧拉出生于牧师家庭,自幼受父亲的影响。
13岁时入读巴塞尔大学,15岁大学毕业,16岁获得硕士学位。
欧拉是18世纪数学界最杰出的人物之一,他不但为数学界作出贡献,更把整个数学推至物理的领域。
他是数学史上最多产的数学家,平均每年写出八百多页的论文,还写了大量的力学、分析学、几何学、变分法等的课本,《无穷小分析引论》、《微分学原理》、《积分学原理》等都成为数学界中的经典著作。
欧拉对数学的研究如此之广泛,因此在许多数学的分支中也可经常见到以他的名字命名的重要常数、公式和定理。
此外,欧拉还涉及建筑学、弹道学、航海学等领域。
欧拉向圣彼得堡科学院提交《哥尼斯堡的七座桥》的论文时,只有29岁,在解答问题的同时,他开创了数学的一个新的分支——图论与几何拓扑。
欧拉是一个天才,在数学史上的地位就像牛顿在物理学的地位一般伟大,28岁时,由于生病,欧拉的右眼失明了。晚年时左眼也失明了。
但是就在双目失明的情况下,欧拉还凭借心算解决了许多的数学问题。
他不光是数学史上里程碑式的人物,同时也是一位物理学家,为物理学的发展铺平了数学的道路。
在他的一生中写出了886本书籍和论文,彼得堡科学院为了整理他的著作,足足忙了47年!
法国数学家拉普拉斯则认为:读读欧拉,他是所有人的老师。
数学史上公认的4名最伟大的数学家分别是:阿基米德、牛顿、欧拉和高斯。
阿基米德有“翘起地球”的豪言壮语,
牛顿因为苹果闻名世界,
高斯少年时就显露出计算天赋,
唯独欧拉没有戏剧性的故事让人印象深刻。
什么样的图形只用一笔就能画出来?笔既不离开纸面,笔迹也不能重复。这实际上是十八世纪一个经典的数学问题:哥尼斯堡七桥问题。
七桥问题
在普鲁士的哥尼斯堡(今俄罗斯加里宁格勒)有一个公园,公园里有七座桥将普雷格尔河中两个岛与与河岸连接起来。

1736年,当地居民举办了一项有意思的健身活动:在星期六作一次走过所有七座桥的散步,每座桥只能经过一次,而且起点与终点必须是同一地点。
有许多人进行了尝试,但是都失败了。
此时当时世界上最伟大的数学家--欧拉 刚好在这里,他敏锐的发现这里蕴藏着深刻的数学内涵,并把它称为一笔画问题。

欧拉把七座桥画作七条线段,并把问题转化为:是否可以通过一笔将这个图形画出来。经过思考,欧拉认为这是不可能的。
不仅如此,欧拉还得出了,哪些图形可以一笔画,哪些不能一笔画的条件。
欧拉把 图形中的 点 分为两种:
如果 过该点的线段 有 偶数条,就称为 偶点;
如果 过该点的线段 有 奇数条,就称为 奇点。
欧拉指出:如果一个图形可以一笔画,那么它的奇点个数一定是 0个 或者 2 个。
如果 奇点个数 是 0个,那么起点 和 终点 是同一个点,从图形中任何一点出发都可以一笔画。
如果 奇点个数是 2 个,那么 只能从 一个奇点 出发,画到 另一个奇点,才能 将图形画出来。
下面解释一下为什么:
1、如果一个点 既不是 起点 也不是 终点,那么线段 经过 该点 时,必然 是 一进一出,线段 成对 出现,一定是 偶点。
2、如果起点和终点是一个点,那么该点有一条 出发线段 和 一条 结束线段,也是偶点。
3、 如果这个点只是出发点,或者只是结束点,才可能是奇点。
所以,如果从一点出发 一笔画 回到 这个点,图形中就 不会有 奇点;如果从一点出发 一笔画到 另一点,图形中就会有 两个 奇点。
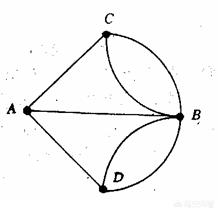
下面再来看看格尼斯堡七桥问题:

可以看出,经过 A、C 或 D 各有3条线段,所以 A、C 和 D 都是奇点;过 B 有 5条 线段,所以 B 也是奇点。所以该图中 共有 4个 奇点,是不能一笔画的。
一笔画定理
⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个奇点为终点。
⒊其他情况的图都不能一笔画出。(奇点数除以二便可算出此图需几笔画成。)
对于一个连通图,通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。
小练习:
请问 “日” 和 “田” 字 可以一笔画吗 ?可以的话,请给出笔画经过的轨迹路线,如果不可以,那么最少需要几笔即可画成,并说明每笔画经过的轨迹路线。^_^
